gkkrlmz
Speculator
- BNB
- 0,00002850
Satoshi Nakamoto tarafından 2008 yılında yazılan manifesto birçok dilden sonra şimdi de Türkçe’ye çevrildi. Bu makalede; Bitcoin makale türkçe pdf, bitcoin whitepaper türkçe pdf, satoshi nakamoto makalesi pdf, satoshi nakamoto manifesto türkçe, bitcoin pdf, satoshi nakamoto bitcoin a peer to peer electronic cash system pdf gibi aramalarınıza cevap bulabilirsiniz.
Bitcoin: Eşten-eşe Elektronik Nakit Ödeme Sistemi
Satoshi Nakamoto
Türkçe’ye Çeviren: bitcoinhaber.net
PDF formatında İngilizce Orijinali: Bitcoin: A Peer-to-Peer Electronic Cash System
Bitmex'te bitcoin ve XRP ile 100 katına kadar kaldıraçlı işlemi %10 komisyon indirim avantajıyla bu linkten üye olarak yapabilirsiniz.
İçerik Rehberi
Tamamen eşten-eşe çalışan bir elektronik para sistemi herhangi bir finansal kurumdan geçmeden bir taraftan diğerine online ödeme gönderilmesini mümkün kılar. Dijital imzalar çözümün bir parçasıdır, ancak mükerrer harcamaları önlemek için hala güvenilir bir üçüncü tarafa ihtiyaç duyuluyorsa temel faydalarını kaybederler. Mükerrer harcama problemine eşler arası ağ kullanarak bir çözüm öneriyoruz. Ağ, işlemleri sürekli uzayan özet fonksiyonu tabanlı bir iş-kanıtı zincirine ekleyerek zaman damgasıyla işaretler ve iş-kanıtını tekrar üretmeden değiştirilemez bir kayıt oluşturur. En uzun zincir sadece karşılaşılan olayların sırasını kanıtlamakla kalmaz aynı zamanda en büyük CPU gücüne sahip havuzdan geldiğini de kanıtlar. CPU gücünün çoğunluğu ağa saldırmak için işbirliği yapmayan düğümlerin kontrolünde olduğu sürece en uzun zinciri üretecekler ve saldırganları alt edeceklerdir. Ağın kendisi çok az bir altyapıya ihtiyaç duyar. Mesajların yayınlanmasında “elden geldiği kadar” kuralı geçerlidir. Düğümler istediklerinde ağdan ayrılabilirler ve dışarıda geçirdikleri sürede yapılan işlemlerin kanıtı olan en uzun iş-kanıtı zincirini kabul ederek tekrar katılabilirler.
Giriş
İnternet üzerinden alışveriş bugün neredeyse tamamen, güvenilir bir üçüncü taraf olarak elektronik ödemeleri işleyen finansal kurumlara bağımlı hale geldi. Bu sistem çoğu işlem için oldukça iyi çalışıyor olsa da hala güvene dayalı bir model olmanın zayıflığını barındırıyor. Finansal kurumlar ihtilaflarda ara buluculuktan kaçamadıklarından tamamen geri dönüşü olmayan işlemler gerçekte mümkün değil. Arabuluculuk hizmetinin gideri işlem giderlerini yükseltir ve mümkün olan en küçük işlem miktarını sınırladığı için küçük ödeme işlemlerini engeller, bunun yanında geri döndürülemeyen hizmetler için geri döndürülemeyen ödeme alma imkanının olmaması daha da masraflıdır. İşlemi geri döndürme ihtimali ile birlikte güvenme ihtiyacı da artar. Satıcılar müşterilerine şüpheyle bakmalı ve başka bir durumda ihtiyaç duyulabilecek bilgiden fazlasını vermeleri için zorlamalıdır. Belli bir oranda dolandırıcılık kaçınılmaz kabul edilir. Bu maliyetler ve ödeme belirsizlikleri yüz yüze alışverişte fiziksel para kullanımıyla giderilebilir ancak güven duyulan bir üçüncü taraf olmadan bir iletişim kanalı üzerinden ödeme yapılabilecek bir mekanizma bulunmamaktadır.İhtiyacımız olan güven yerine kriptografik kanıta dayalı, iki tarafın üçüncü bir güvenilir kişiye gerek duymadan doğrudan birbirleriyle işlem yapabileceği bir elektronik ödeme sistemidir. Geri döndürülmesi imkansıza yakın işlemler satıcıları dolandırıcılıktan koruyacaktır. Alıcıları koruyacak rutin emanetçi mekanizmaları kolaylıkla uygulanabilir. Bu makalede eşten-eşe dağıtık bir zaman damgası sunucusunun işlemlerin tarihsel sırasını hesaba dayalı olarak kanıtlamasını kullanarak mükerrer harcama problemine bir çözüm öneriyoruz. Sistem dürüst düğümler topluca saldırgan düğümlerden daha fazla CPU gücünü ellerinde bulundurduğu sürece güvenlidir.
İşlemler
Elektronik parayı bir dijital imza zinciri olarak tanımlıyoruz. Paranın el değiştirmesi sırasında her sahip parayı bir sonrakine gönderirken kendi dijital imzasıyla bir önceki işlemin özetini (hash) ve bir sonraki sahibin açık anahtarını imzalar ve bu imzayı paranın sonuna ekler. Ödeme alan sahiplik zincirini doğrulamak için imzaları doğrulayabilir.

Elbette buradaki problem ödeme alanın zincirdeki önceki sahiplerden birinin parayı mükerrer olarak kullanmadığını doğrulayamamasıdır. Yaygın bir çözüm, merkezi bir otoritenin (banka, merkez) her işlemin mükerrer harcama olup olmadığını kontrol etmesidir. Her işlemden sonra para merkeze geri döner ve yerine yeni bir para piyasaya sürülür. Sadece merkez tarafından doğrudan piyasaya sürülen paraların mükerrer olarak harcanmadığından emin olabiliriz. Bu çözümdeki sorun para sisteminin tüm kaderinin her işlemin üzerinden geçtiği banka gibi bir merkezi kuruluşun elinde olmasıdır. Ödeme alan kişinin, paranın önceki sahiplerinin önceden işlem imzalamadıklarını doğrulayabileceği bir yönteme ihtiyacımız var. Bizim durumumuzda sadece en eski işlem önemlidir, daha sonraki harcama girişimlerini dikkate almıyoruz. Bir işlemin gerçekleşmediğini kanıtlamanın tek yolu tüm işlemlerden haberdar olmaktır. Merkeze dayalı modelde merkez tüm işlemleri bildiği için hangisinin önce geldiğine karar verebilir. Güvenilen bir taraf olmadan bunu başarabilmek için işlemler açıkça ilan edilmelidir [1] ve katılımcıların işlemlerin gerçekleşme sırası konusunda hemfikir olacağı bir sisteme ihtiyacımız vardır. Ödeme alanın her işlem sırasında harcamanın ilk kez yapıldığı taraf olduğunun diğer düğümlerin çoğu tarafından onaylandığı bir kanıta ihtiyacı vardır.
Zaman Damgası Sunucusu
Önerdiğimiz çözüm bir zaman damgası sunucusuyla başlıyor. Bir zaman damgası sunucusu damgalanmayı bekleyen bir işlem bloğunun özetini alarak bu özeti gazete, Usenet [2-5] gibi mecralarda yayınlar. Zaman damgası mesaj yayınladığı anda verinin özete girdiğinin yani var olduğunun kanıtıdır. Her zaman damgası özetinin içinde bir önceki zaman damgasını barındırarak bir zincir oluşturur ve her eklenti öncekileri güçlendirir.

İş Kanıtı
Eşten-eşe dağıtık bir zaman damgası sunucusu uygulaması için gazete ya da Usenet kullanmaktansa Adam Back’ın Hashcash [6] sistemine benzer bir iş-kanıtı sistemine ihtiyacımız var. İş-kanıtının temelinde SHA-256 gibi bir özet fonksiyonunda özet çıktısının belli bir sayıda 0 biti ile başlamasını sağlayacak bir amaç değerin aranması yatar. Ortalama gerekli iş yükü özette amaçlanan ve tek bir özet hesaplamasıyla sınanabilen 0 bitlerinin sayısı ile üssel olarak orantılıdır.
Zaman damgası ağımız için iş kanıtı modelini, blok özeti istenen sayıda 0 biti ile başlayıncaya kadar bloğun içindeki bir amaç değerinin değiştirilmesi üzerine inşa ediyoruz. İş kanıtını elde edecek CPU tüketimi gerçekleştikten sonra blok aynı işi tekrar yapmadan değiştirilemez. Zincire sonradan eklenen bloklar öncekilere bağlı olduklarından bir bloğu değiştirmek kendinden sonra gelen tüm blokları da tekrar hesaplamayı gerektirecektir.

İş-kanıtı aynı zamanda çoğunluk kararının temsil edilmesi problemini de çözer. Eğer çoğunluk kararı IP adreslerine dayalı bir yöntemle hesaplanıyor olsaydı birçok IP adresine sahip olan kişiler tarafından suistimal edilebilirdi. İş-kanıtı yönteminde 1 CPU 1 Oya eşittir. Çoğunluk kararı en fazla iş kanıtının yapıldığı en uzun zincir tarafından temsil edilir. CPU işlem gücünün çoğunluğu dürüst düğümlerin elindeyse dürüst zincir diğerlerinden daha uzun olacak ve rakip zincirleri alt edecektir. Geçmiş bloklardan birini değiştirmek için saldırganın sonrasında gelen tüm bloklardaki işi tekrar yapması ve dürüst düğümlerin yaptığı işi yakalayıp geçmesi gereklidir. Yazının devamında yeni bloklar eklendikçe daha yavaş bir saldırganın bunlara yetişme olasılığının üssel olarak azaldığını göstereceğiz. Artan donanım hızlarına ve değişken aktif düğüm sayısına ayak uydurmak üzere iş-kanıtı zorluk seviyesi saatte ortalama blok hedefini tutturacak şekilde tekrar ayarlanır. Eğer çok hızlı blok üretiliyorsa zorluk seviyesi yükselir.
Ağ
Ağı işletme adımları şunlardır:
1) Yeni işlemler tüm düğümlere yayılır.
2) Her bir düğüm yeni işlemleri bir blok içinde toplar.
3) Her bir düğüm kendi bloğu içinde bir iş-kanıtı bulmak için çalışır.
4) İş-kanıtını bulan düğüm bunu tüm diğer düğümlere yayar.
5) Diğer düğümler blok içindeki tüm işlemler geçerliyse ve daha önceden harcanmadıysa bloğu kabul ederler.
6) Düğümler bir sonraki bloğu çözmek için çalışmaya koyulduklarında önceki bloğun özetini de yeni bloğa dahil ederler, böylece bloğu kabul ettiklerini göstermiş olurlar.
Düğümler her zaman en uzun zincirin doğru olduğunu kabul ederek uzatmaya çalışırlar. Eğer iki düğüm aynı sıradaki bloğun farklı versiyonlarını aynı anda bulup yayınlarlarsa bazı düğümler birini diğerinden önce alabilir. Bu durumda düğümler ilk aldıkları bloğu doğru kabul ederler ve üzerinde çalışırlar ama diğer dalı da sonradan daha fazla uzama ihtimaline karşılık saklarlar. Beraberlik bir sonraki iş-kanıtı bulunduğunda ve dallardan birisi daha uzun hale geldiğinde bozulmuş olacak, diğer dal üzerinde çalışan düğümler de uzun tarafa geçeceklerdir. Yeni işlemlerin tüm düğümlere ulaşması gerekmez. Yeteri kadar düğüme ulaştıklarında çok geçmeden bir blokta yer alırlar. Blok yayınları mesaj kayıplarına karşı da dayanıklıdır. Eğer bir düğüm bir bloğu alamadıysa bir sonrakini aldığında kayıp olanı fark eder ve istekte bulunur.
Teşvik
Kural gereği bir bloktaki ilk işlem bu bloğu yaratanın sahip olacağı yeni bir parayı dolaşıma çıkardığı özel bir işlemdir. Bu düğümlerin ağı desteklemelerini teşvik eder. Aynı zamanda, para basacak merkezi bir kurum olmadığından paranın dolaşıma katılmasını da sağlar. Sabit bir miktardaki para miktarının sürekli dolaşıma girmesini altın madencilerinin piyasaya yeni altın sürmesine benzetebiliriz. Bizim durumumuzda tüketilen şey CPU işlem gücü ve elektriktir.
Teşvik işlem ücretlerinden de elde edilebilir. Bir işlemin çıktısı girdilerinden küçükse, aradaki fark işlem ücreti olarak işlemi ihtiva eden bloğun teşvik miktarına eklenir. Önceden belirlenmiş bir miktar para tedavüle çıktıktan sonra teşvik tamamen işlem ücretinden elde edilir ve enflasyon sıfıra iner.
Teşvik düğümlerin dürüst kalmalarını sağlar. Eğer açgözlü bir saldırgan bütün dürüst düğümlerden daha fazla işlem gücünü toplamayı başarabilirse bu gücü ödemelerini çalarak insanları dolandırmak için mi yoksa yeni para üretmek için mi kullanacağına karar vermelidir. Oyunu kurallarına uygun oynamayı daha karlı bulmalıdır. Sistemi kandırıp kendi zenginliğinin geçerliğini zedelemektense kurallara uymak ona herkesin toplamından daha fazla yeni para kazandıracaktır.
Disk Alanından Tasarruf
Bir paranın kullanıldığı son işlem yeteri kadar bloğun altında kaldığında öncesindeki harcama işlemleri saklama alanından tasarruf etmek üzere silinebilirler. Bloğun özetini bozmadan bunu sağlamak için işlemler bir Merkle ağacında [7][2][5] tutulur ve sadece kökü bloğun özetine dahil edilir. Eski bloklar ağaç dalları budanarak sıkıştırılabilir. Ara özetlerin saklanmasına gerek yoktur.
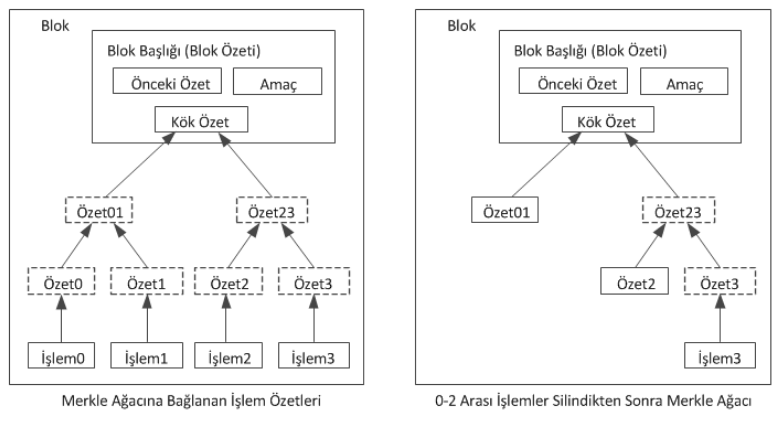
Bir blok başlığı işlemler hariç yaklaşık 80 bayt uzunluğundadır. Her 10 dakikada bir yeni blok üretildiğini varsayarsak 80 bayt * 6 * 24 * 365 = 4.2 MB / yıl eder. 2008 yılında tipik bilgisayar sistemlerinin 2GB RAM ile satıldığı ve Moore yasasına dayanarak senede 1.2GB büyüme öngörüsüyle, blok başlıkları hafızada tutulsa dahi saklama bir sorun olmayacaktır.
Basitleştirilmiş Ödeme Doğrulaması
Tam bir düğüm işletmeden de ödemeleri doğrulamak mümkündür. Kullanıcı sadece en uzun iş-kanıtı zincirine dahil olan blokların başlıklarının bir kopyasını saklamalıdır. En uzun zincire sahip olduğuna kanaat getirinceye kadar ağdaki düğümleri sorgulayarak bu başlıkları toplar ve işlemi damgalandığı bloğa bağlayan Merkle dalını elde eder. İşlemi kendisi doğrulayamaz ama zincirdeki bir yer ile ilişkilendirmekle bir ağ düğümünün kabul ettiğini görür. Ardından eklenen bloklar da ağın işlemi kabul ettiğini onaylarlar.

Bu sebeple, doğrulama dürüst düğümler ağ kontrolünü ellerinde bulundurdukları sürece güvenilirdir. Hesaplama gücünün çoğunluğu saldırganın elindeyse daha savunmasızdır. Ağ düğümleri işlemleri kendileri doğrulayabilirken basitleştirilmiş yöntem saldırganın ağa hakim olduğu süre boyunca ürettiği sahte işlemler ile kandırılabilir. Bu soruna karşı korunma stratejilerinden biri ağ düğümlerinin geçersiz bir bloğu fark ettiklerinde alarm üreterek kullanıcıdan tüm bloğu ve şüpheli işlemleri yüklemesini istemesi olabilir. Sık ödeme alan iş yerleri muhtemelen güvenliklerini sağlamada daha bağımsız olmak ve daha hızlı doğrulama yapabilmek için kendi ağ düğümlerini işletmek isteyeceklerdir.
Değerleri Birleştirme ve Bölme
Her bir parayı teker teker takip etmek mümkün olsa da havale edilecek her kuruş için ayrı ayrı işlem açmak pratik olmazdı. Değerin bölünebilmesi ve birleştirilebilmesi için işlemler birden fazla girdi ve çıktıdan oluşur. Genellikle ya önceki büyük bir işlemden gelen tek bir girdi ya da küçük miktarları birleştiren birden fazla girdi olur. En fazla da iki çıktı olur: Birisi ödeme tutarıdır, diğeri de, varsa, parayı gönderene geri dönen para üstüdür.
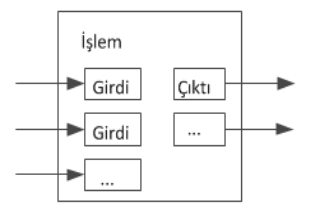
Unutulmamalıdır ki dallanma, yani her bir işlemin birçok işleme bağlı olması ve o işlemlerin de daha da fazla işleme bağlı olmaları burada bir sorun değildir. Hiçbir zaman işlem tarihçesinin tam bir kopyasını çıkartmaya ihtiyaç yoktur.
Gizlilik
Geleneksel bankacılık modeli bilgiye erişim yetkisini ilgili taraflar ve güvenilir bir üçüncü tarafla sınırlayarak bir noktaya kadar gizliliği sağlar. Tüm işlemlerin açık şekilde ilan edilmesi ihtiyacı bu yöntemi kullanışsız bırakır ama bilgi akışını başka bir noktadan keserek hala gizlilik sağlanabilir: Açık anahtarları isimsiz tutarak. Dışarıdan birisinin bir başkasına belli bir miktar gönderdiği izlenebilir ancak işlemi kimin yaptığı bilgisi yoktur. Bu borsaların işlemlerle ilgili açıkladıkları bilgi miktarına benzer. Tek tek her alış satış işleminin zamanı ve miktarı herkesin görebileceği şekilde ilan edilir fakat tarafların kimlikleri gizlidir.
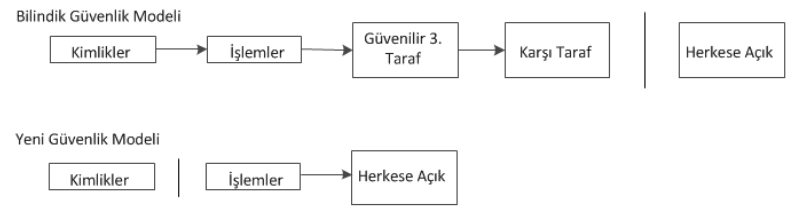
İlave bir bariyer olarak, açık anahtarın sahibi ile ilişkisini gizlemek için her işlemde yeni bir anahtar çifti kullanılmalıdır. Çok girdili işlemlerde bir miktar ilişkilendirme kaçınılmazdır ve işlemin girdilerinin aynı kişiye ait olduğunu açığa çıkarırlar. Korkulan olay anahtarın sahibinin belli olması durumunda aynı kişiye ait diğer işlemlerin de açığa çıkmasıdır.
Hesaplamalar
Dürüst zincirden daha hızlı şekilde alternatif bir zincir oluşturmaya çalışan saldırganın senaryosunu ele alalım. Eğer bunu başarabilse bile bu olay sistemi yoktan para var etmek, ya da hiç sahip olmadığı bir parayı elde etmek gibi keyfi değişikliklere karşı savunmasız hale getirmez. Düğümler geçersiz bir işlemi ödeme olarak kabul etmeyeceklerdir. Dürüst düğümler de bu işlemleri barındıran blokları asla kabul etmeyeceklerdir. Bir saldırgan sadece kendi işlemlerinden birini değiştirerek yakın zamanda harcadığı parayı geri almayı deneyebilir.
Dürüst zincir ile saldırgan arasındaki yarışı Binom Rastgele Yürüyüş şeklinde tariflemek mümkündür. Başarılı olma durumu dürüst zincirin bir blok uzamasıdır ve +1 puan öne geçirir. Başarısızlık durumu da saldırganın zincirini bir blok uzatmasıdır ve aradaki farkı -1 puan kadar azaltır.
Saldırganın belirli bir gecikme farkını kapatabilme olasılığını Kumarbazın İflası problemine benzetebiliriz. Sınırsız krediye sahip bir kumarbazın bir borç ile oyuna başladığını ve başa baş noktasına gelebilmek için sonsuz sayıda deneme yapabileceğini varsayalım. Kumarbazın beraberliğe ulaşma olasılığını ya da saldırganın dürüst zinciri yakalama olasılığını şöyle hesaplayabiliriz [8] :
p = dürüst bir düğümün sıradaki bloğu bulma olasılığı
q = saldırganın sıradaki bloğu bulma olasılığı
qz = saldırganın z blok geriden gelerek beraberliği yakalama olasılığı

p > q varsayımıyla, saldırganın yakalamak zorunda kaldığı blok sayısı arttıkça olasılık üssel olarak azalır. Kendi dezavantajına işleyen olasılıklar karşısında eğer en başlarda şanslı bir dizi hamle yapamazsa daha da geride kaldıkça kazanma ihtimali yok denecek kadar azalır.
Şimdi de yeni bir işlemdeki alacaklının, gönderenin işlemi değiştiremeyeceğinden emin olana dek ne kadar beklemesi gerektiğini ele alalım. Gönderenin alıcıyı para ödediğine bir süreliğine inandırmak isteyen ve bir süre sonra işlemi paranın kendisine geri dönmesi için değiştirmeyi planlayan bir saldırgan olduğunu varsayıyoruz. Bu olay olduğunda alıcı haberdar olacaktır. Ama saldırgan bunun için çok geç olmasını ümit eder.
Alıcı yeni bir çift anahtar üreterek açık anahtarı imzalamadan hemen önce gönderene iletir. Bu şekilde göndericinin önceden bir blok zinciri hazırlaması ve üzerinde çalışarak öne geçtiği şanslı anında işlemi gerçekleştirmesi engellenir. İşlem gönderildiğinde kötü niyetli gönderici gizlice işlemin farklı bir versiyonunu içeren paralel bir zincir üretmek için çalışmaya koyulur.
Alıcı işlemin bir bloğa eklenmesini ve ardından bloğa z blok daha bağlanmasını bekler. Saldırganın tam olarak ne kadar ilerleme kaydedebildiğini bilmiyordur ama dürüst blokların ortalama beklenen zamanda üretildiklerini varsayarsak saldırganın potansiyel ilerleme miktarı beklenen değere göre Poisson dağılımı olur:

Saldırganın hala yetişebilme ihtimalini hesaplamak için her ilerleme miktarının Poisson yoğunluğunu bu noktadan itibaren yetişebilme olasılığı ile çarpıyoruz:

Sonsuz dağılım kuyruğunun toplamını almaktan kaçınmak için tekrar düzenliyoruz.

C koduna dönüştürürsek …
#include <math .h="">
double SaldirganinBasariOlasiligi(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
Birkaç denemenin sonunda gözlemliyoruz ki olasılık z ye bağlı olarak katlanarak azalıyor:
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
P yi %0.1 den küçük değerler için çözdüğümüzde…
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
Sonuç
Güvene dayalı olmayan bir elektronik transfer sistemi önerdik. Dijital imzalardan oluşan sıradan bir para sistemi modeliyle başladık. Bu sistem sahipliği düzgün bir şekilde kontrol edebiliyordu ancak çifte harcama problemini engellemediğinden eksikti. Bunu çözmek için iş kanıtını işlem tarihçesini kaydetmek için kullanan eşten-eşe bir ağ önerdik. Bu tarihçeyi bir saldırganın değiştirmesi işlem gücünün çoğunluğu dürüst düğümlerde olduğu sürece neredeyse imkansızdır. Ağ kendi yapılandırılmamış basitliği içinde sağlamdır. Düğümler aynı anda çok az eş güdüm ile çalışır. Kimlik doğrulamasına gerek yoktur çünkü mesajlar belirli bir yere doğru yönlendirmezler ve sadece diğer düğümlerin ellerinden geldiğince dağıtılır. Düğümler dilediklerinde ağdan ayrılabilirler ve tekrar katılabilirler. İş kanıtı zincirini kendileri ağda yokken olan bitenin kanıtı olarak kabul ederler. İşlem güçleri oranında oy kullanırlar, geçerli bloklar üzerinde çalışarak ve uzamalarını sağlayarak kabul ettiklerini, üzerinde çalışmayarak da reddettiklerini ifade etmiş olurlar. İhtiyaç duyulan tüm kurallar ve teşvikler bu uzlaşma mekanizması ile empoze edilebilir.
Bitcoin: Eşten-eşe Elektronik Nakit Ödeme Sistemi
Satoshi Nakamoto
Türkçe’ye Çeviren: bitcoinhaber.net
PDF formatında İngilizce Orijinali: Bitcoin: A Peer-to-Peer Electronic Cash System
Bitmex'te bitcoin ve XRP ile 100 katına kadar kaldıraçlı işlemi %10 komisyon indirim avantajıyla bu linkten üye olarak yapabilirsiniz.
İçerik Rehberi
- Özet
- Giriş
- İşlemler
- Zaman Damgası Sunucusu
- İş Kanıtı
- Ağ
- Teşvik
- Disk Alanından Tasarruf
- Basitleştirilmiş Ödeme Doğrulaması
- Değerleri Birleştirme ve Bölme
- Gizlilik
- Hesaplamalar
- Sonuç
- Kaynaklar
Tamamen eşten-eşe çalışan bir elektronik para sistemi herhangi bir finansal kurumdan geçmeden bir taraftan diğerine online ödeme gönderilmesini mümkün kılar. Dijital imzalar çözümün bir parçasıdır, ancak mükerrer harcamaları önlemek için hala güvenilir bir üçüncü tarafa ihtiyaç duyuluyorsa temel faydalarını kaybederler. Mükerrer harcama problemine eşler arası ağ kullanarak bir çözüm öneriyoruz. Ağ, işlemleri sürekli uzayan özet fonksiyonu tabanlı bir iş-kanıtı zincirine ekleyerek zaman damgasıyla işaretler ve iş-kanıtını tekrar üretmeden değiştirilemez bir kayıt oluşturur. En uzun zincir sadece karşılaşılan olayların sırasını kanıtlamakla kalmaz aynı zamanda en büyük CPU gücüne sahip havuzdan geldiğini de kanıtlar. CPU gücünün çoğunluğu ağa saldırmak için işbirliği yapmayan düğümlerin kontrolünde olduğu sürece en uzun zinciri üretecekler ve saldırganları alt edeceklerdir. Ağın kendisi çok az bir altyapıya ihtiyaç duyar. Mesajların yayınlanmasında “elden geldiği kadar” kuralı geçerlidir. Düğümler istediklerinde ağdan ayrılabilirler ve dışarıda geçirdikleri sürede yapılan işlemlerin kanıtı olan en uzun iş-kanıtı zincirini kabul ederek tekrar katılabilirler.
Giriş
İnternet üzerinden alışveriş bugün neredeyse tamamen, güvenilir bir üçüncü taraf olarak elektronik ödemeleri işleyen finansal kurumlara bağımlı hale geldi. Bu sistem çoğu işlem için oldukça iyi çalışıyor olsa da hala güvene dayalı bir model olmanın zayıflığını barındırıyor. Finansal kurumlar ihtilaflarda ara buluculuktan kaçamadıklarından tamamen geri dönüşü olmayan işlemler gerçekte mümkün değil. Arabuluculuk hizmetinin gideri işlem giderlerini yükseltir ve mümkün olan en küçük işlem miktarını sınırladığı için küçük ödeme işlemlerini engeller, bunun yanında geri döndürülemeyen hizmetler için geri döndürülemeyen ödeme alma imkanının olmaması daha da masraflıdır. İşlemi geri döndürme ihtimali ile birlikte güvenme ihtiyacı da artar. Satıcılar müşterilerine şüpheyle bakmalı ve başka bir durumda ihtiyaç duyulabilecek bilgiden fazlasını vermeleri için zorlamalıdır. Belli bir oranda dolandırıcılık kaçınılmaz kabul edilir. Bu maliyetler ve ödeme belirsizlikleri yüz yüze alışverişte fiziksel para kullanımıyla giderilebilir ancak güven duyulan bir üçüncü taraf olmadan bir iletişim kanalı üzerinden ödeme yapılabilecek bir mekanizma bulunmamaktadır.İhtiyacımız olan güven yerine kriptografik kanıta dayalı, iki tarafın üçüncü bir güvenilir kişiye gerek duymadan doğrudan birbirleriyle işlem yapabileceği bir elektronik ödeme sistemidir. Geri döndürülmesi imkansıza yakın işlemler satıcıları dolandırıcılıktan koruyacaktır. Alıcıları koruyacak rutin emanetçi mekanizmaları kolaylıkla uygulanabilir. Bu makalede eşten-eşe dağıtık bir zaman damgası sunucusunun işlemlerin tarihsel sırasını hesaba dayalı olarak kanıtlamasını kullanarak mükerrer harcama problemine bir çözüm öneriyoruz. Sistem dürüst düğümler topluca saldırgan düğümlerden daha fazla CPU gücünü ellerinde bulundurduğu sürece güvenlidir.
İşlemler
Elektronik parayı bir dijital imza zinciri olarak tanımlıyoruz. Paranın el değiştirmesi sırasında her sahip parayı bir sonrakine gönderirken kendi dijital imzasıyla bir önceki işlemin özetini (hash) ve bir sonraki sahibin açık anahtarını imzalar ve bu imzayı paranın sonuna ekler. Ödeme alan sahiplik zincirini doğrulamak için imzaları doğrulayabilir.
Elbette buradaki problem ödeme alanın zincirdeki önceki sahiplerden birinin parayı mükerrer olarak kullanmadığını doğrulayamamasıdır. Yaygın bir çözüm, merkezi bir otoritenin (banka, merkez) her işlemin mükerrer harcama olup olmadığını kontrol etmesidir. Her işlemden sonra para merkeze geri döner ve yerine yeni bir para piyasaya sürülür. Sadece merkez tarafından doğrudan piyasaya sürülen paraların mükerrer olarak harcanmadığından emin olabiliriz. Bu çözümdeki sorun para sisteminin tüm kaderinin her işlemin üzerinden geçtiği banka gibi bir merkezi kuruluşun elinde olmasıdır. Ödeme alan kişinin, paranın önceki sahiplerinin önceden işlem imzalamadıklarını doğrulayabileceği bir yönteme ihtiyacımız var. Bizim durumumuzda sadece en eski işlem önemlidir, daha sonraki harcama girişimlerini dikkate almıyoruz. Bir işlemin gerçekleşmediğini kanıtlamanın tek yolu tüm işlemlerden haberdar olmaktır. Merkeze dayalı modelde merkez tüm işlemleri bildiği için hangisinin önce geldiğine karar verebilir. Güvenilen bir taraf olmadan bunu başarabilmek için işlemler açıkça ilan edilmelidir [1] ve katılımcıların işlemlerin gerçekleşme sırası konusunda hemfikir olacağı bir sisteme ihtiyacımız vardır. Ödeme alanın her işlem sırasında harcamanın ilk kez yapıldığı taraf olduğunun diğer düğümlerin çoğu tarafından onaylandığı bir kanıta ihtiyacı vardır.
Zaman Damgası Sunucusu
Önerdiğimiz çözüm bir zaman damgası sunucusuyla başlıyor. Bir zaman damgası sunucusu damgalanmayı bekleyen bir işlem bloğunun özetini alarak bu özeti gazete, Usenet [2-5] gibi mecralarda yayınlar. Zaman damgası mesaj yayınladığı anda verinin özete girdiğinin yani var olduğunun kanıtıdır. Her zaman damgası özetinin içinde bir önceki zaman damgasını barındırarak bir zincir oluşturur ve her eklenti öncekileri güçlendirir.
İş Kanıtı
Eşten-eşe dağıtık bir zaman damgası sunucusu uygulaması için gazete ya da Usenet kullanmaktansa Adam Back’ın Hashcash [6] sistemine benzer bir iş-kanıtı sistemine ihtiyacımız var. İş-kanıtının temelinde SHA-256 gibi bir özet fonksiyonunda özet çıktısının belli bir sayıda 0 biti ile başlamasını sağlayacak bir amaç değerin aranması yatar. Ortalama gerekli iş yükü özette amaçlanan ve tek bir özet hesaplamasıyla sınanabilen 0 bitlerinin sayısı ile üssel olarak orantılıdır.
Zaman damgası ağımız için iş kanıtı modelini, blok özeti istenen sayıda 0 biti ile başlayıncaya kadar bloğun içindeki bir amaç değerinin değiştirilmesi üzerine inşa ediyoruz. İş kanıtını elde edecek CPU tüketimi gerçekleştikten sonra blok aynı işi tekrar yapmadan değiştirilemez. Zincire sonradan eklenen bloklar öncekilere bağlı olduklarından bir bloğu değiştirmek kendinden sonra gelen tüm blokları da tekrar hesaplamayı gerektirecektir.
İş-kanıtı aynı zamanda çoğunluk kararının temsil edilmesi problemini de çözer. Eğer çoğunluk kararı IP adreslerine dayalı bir yöntemle hesaplanıyor olsaydı birçok IP adresine sahip olan kişiler tarafından suistimal edilebilirdi. İş-kanıtı yönteminde 1 CPU 1 Oya eşittir. Çoğunluk kararı en fazla iş kanıtının yapıldığı en uzun zincir tarafından temsil edilir. CPU işlem gücünün çoğunluğu dürüst düğümlerin elindeyse dürüst zincir diğerlerinden daha uzun olacak ve rakip zincirleri alt edecektir. Geçmiş bloklardan birini değiştirmek için saldırganın sonrasında gelen tüm bloklardaki işi tekrar yapması ve dürüst düğümlerin yaptığı işi yakalayıp geçmesi gereklidir. Yazının devamında yeni bloklar eklendikçe daha yavaş bir saldırganın bunlara yetişme olasılığının üssel olarak azaldığını göstereceğiz. Artan donanım hızlarına ve değişken aktif düğüm sayısına ayak uydurmak üzere iş-kanıtı zorluk seviyesi saatte ortalama blok hedefini tutturacak şekilde tekrar ayarlanır. Eğer çok hızlı blok üretiliyorsa zorluk seviyesi yükselir.
Ağ
Ağı işletme adımları şunlardır:
1) Yeni işlemler tüm düğümlere yayılır.
2) Her bir düğüm yeni işlemleri bir blok içinde toplar.
3) Her bir düğüm kendi bloğu içinde bir iş-kanıtı bulmak için çalışır.
4) İş-kanıtını bulan düğüm bunu tüm diğer düğümlere yayar.
5) Diğer düğümler blok içindeki tüm işlemler geçerliyse ve daha önceden harcanmadıysa bloğu kabul ederler.
6) Düğümler bir sonraki bloğu çözmek için çalışmaya koyulduklarında önceki bloğun özetini de yeni bloğa dahil ederler, böylece bloğu kabul ettiklerini göstermiş olurlar.
Düğümler her zaman en uzun zincirin doğru olduğunu kabul ederek uzatmaya çalışırlar. Eğer iki düğüm aynı sıradaki bloğun farklı versiyonlarını aynı anda bulup yayınlarlarsa bazı düğümler birini diğerinden önce alabilir. Bu durumda düğümler ilk aldıkları bloğu doğru kabul ederler ve üzerinde çalışırlar ama diğer dalı da sonradan daha fazla uzama ihtimaline karşılık saklarlar. Beraberlik bir sonraki iş-kanıtı bulunduğunda ve dallardan birisi daha uzun hale geldiğinde bozulmuş olacak, diğer dal üzerinde çalışan düğümler de uzun tarafa geçeceklerdir. Yeni işlemlerin tüm düğümlere ulaşması gerekmez. Yeteri kadar düğüme ulaştıklarında çok geçmeden bir blokta yer alırlar. Blok yayınları mesaj kayıplarına karşı da dayanıklıdır. Eğer bir düğüm bir bloğu alamadıysa bir sonrakini aldığında kayıp olanı fark eder ve istekte bulunur.
Teşvik
Kural gereği bir bloktaki ilk işlem bu bloğu yaratanın sahip olacağı yeni bir parayı dolaşıma çıkardığı özel bir işlemdir. Bu düğümlerin ağı desteklemelerini teşvik eder. Aynı zamanda, para basacak merkezi bir kurum olmadığından paranın dolaşıma katılmasını da sağlar. Sabit bir miktardaki para miktarının sürekli dolaşıma girmesini altın madencilerinin piyasaya yeni altın sürmesine benzetebiliriz. Bizim durumumuzda tüketilen şey CPU işlem gücü ve elektriktir.
Teşvik işlem ücretlerinden de elde edilebilir. Bir işlemin çıktısı girdilerinden küçükse, aradaki fark işlem ücreti olarak işlemi ihtiva eden bloğun teşvik miktarına eklenir. Önceden belirlenmiş bir miktar para tedavüle çıktıktan sonra teşvik tamamen işlem ücretinden elde edilir ve enflasyon sıfıra iner.
Teşvik düğümlerin dürüst kalmalarını sağlar. Eğer açgözlü bir saldırgan bütün dürüst düğümlerden daha fazla işlem gücünü toplamayı başarabilirse bu gücü ödemelerini çalarak insanları dolandırmak için mi yoksa yeni para üretmek için mi kullanacağına karar vermelidir. Oyunu kurallarına uygun oynamayı daha karlı bulmalıdır. Sistemi kandırıp kendi zenginliğinin geçerliğini zedelemektense kurallara uymak ona herkesin toplamından daha fazla yeni para kazandıracaktır.
Disk Alanından Tasarruf
Bir paranın kullanıldığı son işlem yeteri kadar bloğun altında kaldığında öncesindeki harcama işlemleri saklama alanından tasarruf etmek üzere silinebilirler. Bloğun özetini bozmadan bunu sağlamak için işlemler bir Merkle ağacında [7][2][5] tutulur ve sadece kökü bloğun özetine dahil edilir. Eski bloklar ağaç dalları budanarak sıkıştırılabilir. Ara özetlerin saklanmasına gerek yoktur.
Bir blok başlığı işlemler hariç yaklaşık 80 bayt uzunluğundadır. Her 10 dakikada bir yeni blok üretildiğini varsayarsak 80 bayt * 6 * 24 * 365 = 4.2 MB / yıl eder. 2008 yılında tipik bilgisayar sistemlerinin 2GB RAM ile satıldığı ve Moore yasasına dayanarak senede 1.2GB büyüme öngörüsüyle, blok başlıkları hafızada tutulsa dahi saklama bir sorun olmayacaktır.
Basitleştirilmiş Ödeme Doğrulaması
Tam bir düğüm işletmeden de ödemeleri doğrulamak mümkündür. Kullanıcı sadece en uzun iş-kanıtı zincirine dahil olan blokların başlıklarının bir kopyasını saklamalıdır. En uzun zincire sahip olduğuna kanaat getirinceye kadar ağdaki düğümleri sorgulayarak bu başlıkları toplar ve işlemi damgalandığı bloğa bağlayan Merkle dalını elde eder. İşlemi kendisi doğrulayamaz ama zincirdeki bir yer ile ilişkilendirmekle bir ağ düğümünün kabul ettiğini görür. Ardından eklenen bloklar da ağın işlemi kabul ettiğini onaylarlar.
Bu sebeple, doğrulama dürüst düğümler ağ kontrolünü ellerinde bulundurdukları sürece güvenilirdir. Hesaplama gücünün çoğunluğu saldırganın elindeyse daha savunmasızdır. Ağ düğümleri işlemleri kendileri doğrulayabilirken basitleştirilmiş yöntem saldırganın ağa hakim olduğu süre boyunca ürettiği sahte işlemler ile kandırılabilir. Bu soruna karşı korunma stratejilerinden biri ağ düğümlerinin geçersiz bir bloğu fark ettiklerinde alarm üreterek kullanıcıdan tüm bloğu ve şüpheli işlemleri yüklemesini istemesi olabilir. Sık ödeme alan iş yerleri muhtemelen güvenliklerini sağlamada daha bağımsız olmak ve daha hızlı doğrulama yapabilmek için kendi ağ düğümlerini işletmek isteyeceklerdir.
Değerleri Birleştirme ve Bölme
Her bir parayı teker teker takip etmek mümkün olsa da havale edilecek her kuruş için ayrı ayrı işlem açmak pratik olmazdı. Değerin bölünebilmesi ve birleştirilebilmesi için işlemler birden fazla girdi ve çıktıdan oluşur. Genellikle ya önceki büyük bir işlemden gelen tek bir girdi ya da küçük miktarları birleştiren birden fazla girdi olur. En fazla da iki çıktı olur: Birisi ödeme tutarıdır, diğeri de, varsa, parayı gönderene geri dönen para üstüdür.
Unutulmamalıdır ki dallanma, yani her bir işlemin birçok işleme bağlı olması ve o işlemlerin de daha da fazla işleme bağlı olmaları burada bir sorun değildir. Hiçbir zaman işlem tarihçesinin tam bir kopyasını çıkartmaya ihtiyaç yoktur.
Gizlilik
Geleneksel bankacılık modeli bilgiye erişim yetkisini ilgili taraflar ve güvenilir bir üçüncü tarafla sınırlayarak bir noktaya kadar gizliliği sağlar. Tüm işlemlerin açık şekilde ilan edilmesi ihtiyacı bu yöntemi kullanışsız bırakır ama bilgi akışını başka bir noktadan keserek hala gizlilik sağlanabilir: Açık anahtarları isimsiz tutarak. Dışarıdan birisinin bir başkasına belli bir miktar gönderdiği izlenebilir ancak işlemi kimin yaptığı bilgisi yoktur. Bu borsaların işlemlerle ilgili açıkladıkları bilgi miktarına benzer. Tek tek her alış satış işleminin zamanı ve miktarı herkesin görebileceği şekilde ilan edilir fakat tarafların kimlikleri gizlidir.
İlave bir bariyer olarak, açık anahtarın sahibi ile ilişkisini gizlemek için her işlemde yeni bir anahtar çifti kullanılmalıdır. Çok girdili işlemlerde bir miktar ilişkilendirme kaçınılmazdır ve işlemin girdilerinin aynı kişiye ait olduğunu açığa çıkarırlar. Korkulan olay anahtarın sahibinin belli olması durumunda aynı kişiye ait diğer işlemlerin de açığa çıkmasıdır.
Hesaplamalar
Dürüst zincirden daha hızlı şekilde alternatif bir zincir oluşturmaya çalışan saldırganın senaryosunu ele alalım. Eğer bunu başarabilse bile bu olay sistemi yoktan para var etmek, ya da hiç sahip olmadığı bir parayı elde etmek gibi keyfi değişikliklere karşı savunmasız hale getirmez. Düğümler geçersiz bir işlemi ödeme olarak kabul etmeyeceklerdir. Dürüst düğümler de bu işlemleri barındıran blokları asla kabul etmeyeceklerdir. Bir saldırgan sadece kendi işlemlerinden birini değiştirerek yakın zamanda harcadığı parayı geri almayı deneyebilir.
Dürüst zincir ile saldırgan arasındaki yarışı Binom Rastgele Yürüyüş şeklinde tariflemek mümkündür. Başarılı olma durumu dürüst zincirin bir blok uzamasıdır ve +1 puan öne geçirir. Başarısızlık durumu da saldırganın zincirini bir blok uzatmasıdır ve aradaki farkı -1 puan kadar azaltır.
Saldırganın belirli bir gecikme farkını kapatabilme olasılığını Kumarbazın İflası problemine benzetebiliriz. Sınırsız krediye sahip bir kumarbazın bir borç ile oyuna başladığını ve başa baş noktasına gelebilmek için sonsuz sayıda deneme yapabileceğini varsayalım. Kumarbazın beraberliğe ulaşma olasılığını ya da saldırganın dürüst zinciri yakalama olasılığını şöyle hesaplayabiliriz [8] :
p = dürüst bir düğümün sıradaki bloğu bulma olasılığı
q = saldırganın sıradaki bloğu bulma olasılığı
qz = saldırganın z blok geriden gelerek beraberliği yakalama olasılığı
p > q varsayımıyla, saldırganın yakalamak zorunda kaldığı blok sayısı arttıkça olasılık üssel olarak azalır. Kendi dezavantajına işleyen olasılıklar karşısında eğer en başlarda şanslı bir dizi hamle yapamazsa daha da geride kaldıkça kazanma ihtimali yok denecek kadar azalır.
Şimdi de yeni bir işlemdeki alacaklının, gönderenin işlemi değiştiremeyeceğinden emin olana dek ne kadar beklemesi gerektiğini ele alalım. Gönderenin alıcıyı para ödediğine bir süreliğine inandırmak isteyen ve bir süre sonra işlemi paranın kendisine geri dönmesi için değiştirmeyi planlayan bir saldırgan olduğunu varsayıyoruz. Bu olay olduğunda alıcı haberdar olacaktır. Ama saldırgan bunun için çok geç olmasını ümit eder.
Alıcı yeni bir çift anahtar üreterek açık anahtarı imzalamadan hemen önce gönderene iletir. Bu şekilde göndericinin önceden bir blok zinciri hazırlaması ve üzerinde çalışarak öne geçtiği şanslı anında işlemi gerçekleştirmesi engellenir. İşlem gönderildiğinde kötü niyetli gönderici gizlice işlemin farklı bir versiyonunu içeren paralel bir zincir üretmek için çalışmaya koyulur.
Alıcı işlemin bir bloğa eklenmesini ve ardından bloğa z blok daha bağlanmasını bekler. Saldırganın tam olarak ne kadar ilerleme kaydedebildiğini bilmiyordur ama dürüst blokların ortalama beklenen zamanda üretildiklerini varsayarsak saldırganın potansiyel ilerleme miktarı beklenen değere göre Poisson dağılımı olur:
Saldırganın hala yetişebilme ihtimalini hesaplamak için her ilerleme miktarının Poisson yoğunluğunu bu noktadan itibaren yetişebilme olasılığı ile çarpıyoruz:
Sonsuz dağılım kuyruğunun toplamını almaktan kaçınmak için tekrar düzenliyoruz.
C koduna dönüştürürsek …
#include <math .h="">
double SaldirganinBasariOlasiligi(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
Birkaç denemenin sonunda gözlemliyoruz ki olasılık z ye bağlı olarak katlanarak azalıyor:
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
P yi %0.1 den küçük değerler için çözdüğümüzde…
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
Sonuç
Güvene dayalı olmayan bir elektronik transfer sistemi önerdik. Dijital imzalardan oluşan sıradan bir para sistemi modeliyle başladık. Bu sistem sahipliği düzgün bir şekilde kontrol edebiliyordu ancak çifte harcama problemini engellemediğinden eksikti. Bunu çözmek için iş kanıtını işlem tarihçesini kaydetmek için kullanan eşten-eşe bir ağ önerdik. Bu tarihçeyi bir saldırganın değiştirmesi işlem gücünün çoğunluğu dürüst düğümlerde olduğu sürece neredeyse imkansızdır. Ağ kendi yapılandırılmamış basitliği içinde sağlamdır. Düğümler aynı anda çok az eş güdüm ile çalışır. Kimlik doğrulamasına gerek yoktur çünkü mesajlar belirli bir yere doğru yönlendirmezler ve sadece diğer düğümlerin ellerinden geldiğince dağıtılır. Düğümler dilediklerinde ağdan ayrılabilirler ve tekrar katılabilirler. İş kanıtı zincirini kendileri ağda yokken olan bitenin kanıtı olarak kabul ederler. İşlem güçleri oranında oy kullanırlar, geçerli bloklar üzerinde çalışarak ve uzamalarını sağlayarak kabul ettiklerini, üzerinde çalışmayarak da reddettiklerini ifade etmiş olurlar. İhtiyaç duyulan tüm kurallar ve teşvikler bu uzlaşma mekanizması ile empoze edilebilir.
